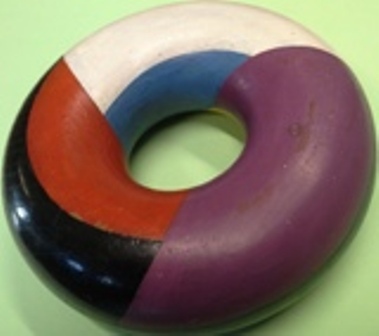
Modell einer Torusfläche mit einer Landkarte, deren Einfärbung 7 Farben benötigt.
Mit Ölfarben bemalter gedrechselter Holztorus.
Durchmesser 12 cm, Höhe 4 cm
Entstehungszeit zwischen 1925 und 1955
Aus der Historischen Sammlung der Fachbibliothek Mathematik, Statistik und Informatik
Es ist eine alte Erfahrung von Kartographen, dass man mit 4 Farben auskommt (aber oft auch alle 4 Farben benötigt), wenn man eine Landkarte in der Ebene oder auf der Kugel so einfärbt, dass Länder, die eine gemeinsame Grenze haben, mit verschiedenen Farben gefärbt werden (zwei Länder, die nur einen Eckpunkt gemeinsam haben, können dabei die gleiche Farbe erhalten). Das auch mathematisch streng zu beweisen, ist sehr lange ein ungelöstes Problem gewesen. Erst 1976 konnte ein Beweis erbracht werden, in den aber umfangreiche Computerrechnungen eingebaut sind. Es war dies der erste "Computerbeweis", für dessen Durchführung ganz neue symbolische Berechnungsverfahren entwickelt werden mussten, die die Grundlage für die heutigen Computeralgebrasysteme geworden sind.
Ähnliche Färbungsprobleme für andere Flächentypen sind wesentlich einfacher zu lösen. Ein Beispiel ist der Torus, wo man immer mit 7 Farben auskommt, wo es aber auch Landkarten gibt, für deren Färbung man alle 7 Farben braucht. Eine solche Landkarte zeigt unser Modell.
Text: Hans-Dominik Schwabl, Fotos: Irene Schachl